Morteza Karimzadeh Parizia, Farshid Keynia*ᵇ, Amid khatibi Bardsiriª
a Department of Computer Engineering, Kerman Branch, Islamic Azad University, Kerman, Iran;
b Department of Energy Management and Optimization, Institute of Science and High Technology and Environmental Sciences, Graduate University of Advanced Technology, Kerman, Iran;(Communicated by J. Vahidi)
Özet
Doğadan ilham alan meta-sezgisel algoritmalar basitlikleri ve esnekliklerinden dolayı mühendislik planlamalarının optimizasyonu ve gerçek dünya problemlerini uyarlayarak çözmek amacıyla araştırmacılar için ilginç bir konu olmuştur. Bu çalışma da Woodpecker Mating Algorithm (WMA) olarak adlandırılan doğadan ilham alan yeni bir arama algoritması sunulmakta ve zorlu problemlere yapısal optimizasyon olarak uygulanmaktadır. WMA ağaçkakanların çiftleşme davranışlarını taklit eden nüfusa dayalı bir meta-sezgisel algoritmadır. Ağaçkakanların nüfusu WMA’ de dişi ve erkek gruplar olarak bölünür. Dişi ağaçkakanlar davul sesinin yoğunluğunu baz alarak erkek ağaçkakanlara yaklaşır. WMA ve diğer meta-sezgisel algoritmalar arasında 19 kıyaslama fonksiyonu (tek modlu, çok modlu, birleşik fonksiyonlar) kullanılarak verimlilik karşılaştırılması yapılmıştır. Dahası, WMA’ in performansı 13 yüksek boyutlu çok modlu ve tek modlu kıyaslama fonksiyonları kullanılarak 8 en iyi meta-sezgisel algoritmayla karşılaştırılmıştır. Değerlendirmeler ve istatistiksel sonuçlar gösterir ki WMA algoritması vaat edilen sonuçları ve en yeni algoritmalardan daha iyi performans gösterir ve literatürde kullanılan kıyaslama fonksiyonlarının çoğunda önerilen popüler algoritmaları sunar. Dahası, diğer değerlendirilen algoritmalarla karşılaştırıldığın da istatistiksel önemli bir fark gözlemlenmiştir. Önerilen algoritma dışbükey olmayan, ayrılmaz ve ölçeklenebilir problemler için önemli sonuçlar üretmiştir.
Giriş
Optimizasyon çıktıyı büyültmek ya da küçültmek için tüm olası değerlerden özel bir sistem parametreleri için en uygun değerleri elde etme sürecidir. Optimizasyon tekniklerinin gelişimine yol açtığı ve aynı zamanda araştırmacılar için merak uyandıran alanlar belirebileceğinden optimizasyon problemi bütün araştırma alanlarında incelenebilir [1]. Son 20 yılda optimizasyon problemlerini çözmek amacıyla meta-sezgisel algoritmalara karşı büyüyen bir ilgi olmuştur [2]. Meta-sezgisel algoritmalar problemi siyah bir kutu gibi değerlendirdiği için popülerdir [1,3]. Rastgele doğalarından dolayı yerel uygunluktan kaçınırlar [2,4]. Sonuç olarak onları öğrenmek ve uygulamak kolaydır [5,6]. Meta-sezgisel algoritmalar çoğunlukla doğal organizmaların kurallarını baz aldığı için doğadan ilham alan algoritmalar olarak adlandırılır [7]. Meta-sezgisel algoritmalar taklidi yapılan fenomenin doğasına bağlı olarak dört sınıf şeklinde kategorize edilebilir: evrimsel algoritmalar, fiziksel tabanlı algoritmalar, sürü zekası algoritmalar, insan davranışından ilham almış algoritmalar [2].
Evrimsel algoritmalar (EA) genellikle çevresel şartlara uyum sağlayan ve gelişen canlı organizmaların yetenekleriyle ilişkili doğanın Darwin prensiplerinden ilham alan belli optimizasyon algoritmalarıdır. Örneğin; Genetik Algoritma (GA) [8,9], Diferansiyel Evrim (DE) [10], Evrimsel Programlama (EP), Evrim Stratejisi (ES) [11], evrimsel algoritmalardır. İkinci sınıf fiziksel tabanlı teknikleri içerir. Bu optimizasyon uygulamaları genellikle fizik kanunlarının simülasyonudur. Örneğin, onlar harekete geçmeyi, yer çekimini, radyasyonu, elektromanyetiği, ağırlığı kullanır [5]. Çoklu Evren Optimizasyonu (MVO) [3], Benzetimli Tavlama (SA) [12], Isı Değişimi Optimizasyonu (TEO) [13] ve Oryantasyon Arama Algoritmaları (OSA) [14] fiziksel tabanlı algoritmalara örnektir. Meta-sezgisel algoritmaların üçüncü sınıfı insan davranışlarından ilham almış algoritmalardır. Örnek olarak Armoni Arama (HS) [8, 15], Beyin Fırtınası Optimizasyon Algoritması (BSOA) [16], Emperyalist Rekabet Algoritması (ICA) [17], Böbrekten Esinlenen Algoritma (KA) [18], İç Arama Algoritması (ISA) [19], Single Seekers Society (SSS) [20], Sinüs Kosinüs Algoritması (SCA) [21], Zayıf ve Zengin Optimizasyon algoritması (PRO) [22], Grup Öğretimi Optimizasyon Algoritması (GTOA) [23] ve Öğrenme Öğretimi Tabanlı Optimizasyon (TLBO) [24].
Dördüncü sınıf optimizasyon problemlerini çözmek için kullanılan dağıtılmış zeka modeli olan sürü zekasıdır (SI). SI böcek sürülerinin ve diğer hayvan sürülerinin kollektif davranışlarından esinlenir. SI genellikle bölgesel çevreyle ve birbirleriyle faaliyet gösteren belli bir grubun basit bir popülasyonunu oluşturur. Bu kuruluş çok sınırlı yeteneklerle çok komplike görevleri tamamlayarak hayatta kalmak için iş birliği yapar [25]. Parçacık Sürüsü Optimizasyonu (PSO) [26, 27], Yapay Arı Kolonisi (ABC) [28], Karınca Kolonisi Optimizasyonu (ACO) [29], Satin Bowerbird Optimizer (SBO) [30], Yusufçuk Algoritması (DA) [31], Gri Kurt Doktoru (GWO) [5], Güve-Alev Optimizasyonu (MFO) [32], Yarasa Algoritması (BA) [33], Ateşböceği Algoritması (FA) [34], Guguk Arama (CS) [35], Karınca Lion Optimizer (ALO) [4], Whale Optimization Algorithm [2], Harris Hawks Optimizer (HHO) [36],Karga Arama Algoritması (SCA) [37, 38], Eşek ve Kaçakçı Optimizasyon Algoritması (SDO) [39] ve Yapay Acari Optimizasyonu (AAO) [40] SI algoritmalarıdır.
Keşif ve istismar nüfusa dayalı meta-sezgisel algoritmaların ortak noktalarıdır [41]. Keşif aşamalarının bütün araştırma alanlarını keşfetmek için belli mekanizmalarla donatılmış bir algoritma olmalıdır. Aslında, araştırma uzayında gelecek vaat eden alanlar bu aşamada belirlenir [3]. Keşif küresel seviyede problemi analiz etmeyi ve en iyi küresel çözümle araştırma uzayında belli alanları tanımlamayı içerir. İstismar aşamaları keşiften sonra gelir. Keşif aşaması içinde bulunan gelecek vaat eden alan analizinin bir süreci olarak tanımlanabilir [2]. İstismar aşaması bölgesel araştırmayı vurgular ve algoritma keşif aşamasında bulunan gelecek vaat eden alanı belli bir noktada toplar [3]. Keşif ve istismar iki zıt dönüm noktasıdır. Aşamanın cesaret veren sonuçları diğer sonuçları azaltır. İki dönüm noktası arasındaki uygun denge nüfus tabanlı algoritmaların kullanımıyla en uygun küresel doğru tahmini garanti edebilir [32].
Bu çalışma da alışılmışın dışında doğadan esinlenen meta-sezgisel algoritma ilk kez ağaçkakanların çiftleşme davranışlarına dayandırılarak kullanılmıştır. Ağaçkakanlar seks karşısında ilgi çekmek için ağaçları gagalarlar. Gagalamak ses dalgası üretir. Fizik kurallarına göre ses dalgaları çevre içinde çoğalır bu yüzden diğer ağaçkakanlar onları duyar. Böylece fiziksel nicelik dinleyici tarafından alınan sesin miktarına bağlı olan ses yoğunluğu olarak belirlenir. Bu gibi kavramlar önerilen algoritmalar için ilham verir.
Bu çalışmanın geri kalanı dört bölüm içerir. İkinci bölümde, ağaçkakanların çiftleşme algoritması tanıtıldı. Üçüncü bölümde önerilen algoritmayı değerlendirmek için matematiksel kıyaslama fonksiyonları kullanıldı. Son olarak dördüncü bölümde gelecek çalışmalar için öneriler ve sonuç sunuldu.
2. Ağaçkakan Çiftleşme Algoritması
Ağaçkakanlar şahane kuşlardır. Onların yaklaşık olarak 200 farklı türü vardır. Ağaçkakanlar iletişim için özel bir strateji kullanırlar. Bu yöntem davul çalma ya da ağaç gövdesini gagalama olarak adlandırılır. Davul çalma ağaçkakanlara özel fırsatlar sağlar. Onlar ağacın gövdesinde yuva yapmak ve böceklerle ya da reçineyle beslenmek için delik açarlar. Böyle yaparak onlar diğer ağaçkakanlarla iletişim kurabilir, yaşam alanlarını gösterebilir ve düşmanlarını korkutabilirler. Fakat, davul çalmanın en önemli amacı çiftleşme sezonunda eş çekmektir [43]. Aslında davul çalma çiftleşme sezonunda cinsiyet içi bir yarışmadır. Erkek ağaçkakanlar dişi ağaçkakanları etkilemek için davul çalarak birbirleriyle yarışır. Dişi ağaçkakan eşini seçmeden önce davul çalma seslerini iyice dinler ve içgüdüsel olarak analiz eder. Sonra en yüksek kaliteye sahip ses onu cezbeder ve o davul çalmanın kaynağına doğru uçar. Davul çalma oranları farklı türlerde farklılık gösterir. Büyük türler için düşer ve onlar bunun yerine yüksek sesli telefonlar kullanırlar. Fakat davul çalma uzun mesafe iletişimi için fonetik olmayan ana araçtır. WMA algoritması kırmızı karınlı ağaçkakanların çiftleşme davranışından esinlenmiştir [44]. Önerilen algoritmada davul çalmanın sadece ağaçkakanlarla bir iletişim aracı olduğu farz edilir.
Çiftleşme sezonunun başında erkek ağaçkakanlar davul çalmaya başlar. Erkek ağaçkakan tarafından üretilen sesin kalitesi dişi ağaçkakanı cezbeden muhteşem bir efekte sahiptir. Diğer hayvanlar gibi ağaçkakanlarda eşlerini etkilemeye ve en iyi eşi seçmeye çalışır. Davul çalmak için yüksek yeterliliğe sahip kuşlar daha güçlü yüksek kaliteli davullar üretebilir ve ideal eşler olarak saygındırlar. Onların davulları daha uzakta duyulabilir ve daha fazla dişi ağaçkakanı etkileyebilir. O zaman dişi ağaçkakanlar kaynaktan etkilenirler, çünkü onlar için daha güçlü ses erkek ağaçkakanın daha iyi yiyecek bulabilmesini, yuva yapabilmesini ve taklit edebilmesini ve onların eş olarak daha iyi seçenek olabileceğini ifade eder. Sonuç olarak, erkek ağaçkakanların davullarının akustik gücü (ses yoğunluğu), dişi kuşları etkilemek için onların yeteneklerini gösterir. Diğer bir yandan, dişi ağaçkakanların erkek ağaçkakanlara doğru hareketinin büyüklüğü duydukları sesin kalitesine bağlıdır. Daha güçlü ses onu üreten erkek ağaçkakana en yakın dişi ağaçkakana ulaşır. Güçlü ya da yüksek kaliteli sesin aşağıda açıklandığı gibi sesin yoğunluğunun fiziksek miktarını ifade etmesi kayda değerdir.
Erkek kuşun sesinden etkilenen bir dişi ağaçkakan ona doğru hareket eder ve ona yaklaşır. Bu süreç her seferinde birkaç kez ya da birkaç gün aralıklarla devam eder, dişi ağaçkakan erkek ağaçkakana daha çok yaklaşır. Erkek ağaçkakanın farklı zaman aralıklarındaki davul çalma performansı ve periyodik davullar dişi kuşa adım adım iletilir. Bu yaklaşım evrimsel sürece benzer ve her bir tekrarlanmayla dişi kuş erkek kuşa daha çok yaklaşır. Başka bir deyişle, erkek ağaçkakan ağaca vurduğunda ses diğer dişi kuşların kulağına ve çevreye iletilir, böylelikle onlar erkek kuşa doğru hareket eder. Erkek kuşun konumu hareketin temelidir çünkü dişi kuşlar erkek kuşun davulundan elde ettikleri bilgilere dayanarak ona doğru hareket eder, bu süreç içinde erkek kuş ve dişi kuş arasında bilgi akışı ve iletişim metodu vardır. Bu yüzden bu süreç sürü zekası davranışıdır. Doğa da çiftleşme sezonunun başında birçok erkek ağaçkakan eş olarak dişi ağaçkakanları etkilemek için davul çalmaya başlar. Sonuç olarak, her bir zaman aralığında aynı anda birkaç erkek ağaçkakanın davul çalma sesini duyarlar. Önceki paragrafın başında değindiğimiz gibi dişi ağaçkakanlar en iyi eşi ararlar. Ama eğer diğer erkek ağaçkakan dişi kuşa yakınsa, dişi kuş bu erkek kuştan etkilenecektir çünkü sessin kaynağı daha kısa mesafede olduğu için en kaliteli davul sesi olacaktır.
2.1. Sesin Yoğunluğu
Ses dalgası fiziğinde [45] alınan ses, ses yoğunluğu olarak adlandırılan niceliğe bağlıdır. Bir seviyenin ses yoğunluğu (SI) seviyeyi aşan ya da seviyeye ulaşan ortalama enerji değişimleridir. Ses yoğunluğu aşağıdaki eşitlikle hesaplanır (2.1):
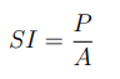
Bu eşitlikte, P sesin gücü, A sesin toplandığı alandır. Sesin gerçek kaynağından mesafe üzerindeki ses yoğunluğu değişimlerinin ne kadar olduğunu saptamak genellikle karmaşıktır. Bazı kaynaklar (hoparlör gibi) sesi sadece bir yönden gönderebilir. Çevrede genellikle aktarmasız ses dalgalarının üst üste gelmesiyle bazı yankılar oluşur. Fakat ekolar bazı durumlarda göz ardı edilebilir. Sesin kaynağını her yönde ses yoğunluğuyla izotropik bir yolda yayılan ses noktası olarak farz edebilirler (Bu varsayım ağaçkakanlar için doğrudur.). Ek olarak ses dalgalarının mekanik enerjisi (P) kaynaktan dalgalar yayıldığında korunur. Eğer çalışma sahası kaynağın çevresinin yarıçapı olarak farz edilirse, kaynaktan yayılan tüm enerji çalışma alanının yüzey alanına doğru geçmelidir. Böylece, çevre boyunca ses dalgalarının enerji transfer oranı kaynağın ses dalgası üretme oranına eşit olabilir. Sonuç olarak, ses yoğunluğu (SI) eşitlik olarak aşağıdaki gibi açıklanır (2.2):
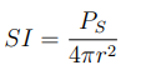
Çalışma sahasının alanı 4πr2 ‘dir. Eşitliğe (2.2) göre izotropik nokta kaynağının ses yoğunluğu mesafenin karesine (r2) göre azalır. Böylece alınan sesin yoğunluğu nesne ve kaynak arasındaki mesafeye oldukça bağlıdır. En kısa mesafede en yüksek ve en kaliteli ses alınacaktır. Öklit uzaklığı aşağıdaki eşitliğe göre hesaplanır (2.3).
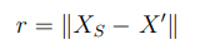
Xs kaynakta toplanan sesin konumu ve X’ dinleyicilerin konumudur. Dişi ağaçkakanların ses yoğunluğunu baz alarak erkek ağaçkakanlara doğru uçtuğu farz edilmiştir (I). Bir diğer asıl faktör mesafedir. Alınan sesin yoğunluğu ağaçkakanlar arasındaki mesafeye de bağlıdır.
2.2 WMA Algoritması Varsayımları
WMA algoritması bahsi geçen kavramlardan esinlenir ve aşağıdaki varsayımlara dayanır.
1. Ağaçkakanlar için iletişimin tek yolu davul çalmayla iletilen sestir.
2. Bütün dişi ağaçkakanlar her mesafe için en uygun erkek ağaçkakanın davul sesini duyar ve etkilenir.
3. Erkek ağaçkakanların zindeliği hedef fonksiyonlar baz alarak hesaplanır.
4. WMA algoritmasında zindeliğin çekicilik faktörü olduğu düşünülür. Dişi ağaçkakanlar daha nitelikli erkek ağaçkakanlardan etkilenir. En iyi ağaçkakan gpop olarak adlandırılır.
5. Dişi ağaçkakanların hangi oranda erkek kuştan etkilendiği duyduğu davulun ses yoğunluğuna bağlıdır. Diğer yandan akustik dalgalar açısından fizik kurallarına göre cezbetme oranı kaynaktan uzaklaştıkça düşer. Erkek ağaçkakanlar için en yakın mesafede cezbetme oranı daha yüksektir.
6. WMA algoritmasında, ağaçkakanların nüfusu erkek ve dişi ağaçkakanların zindelik düzeyi olarak düşünülür. Erkek ağaçkakanların nüfusu keşfin başlarında fazladır (çünkü çiftleşme sezonunun başında bekar erkek ağaçkakanların sayısı fazladır). Fakat bu nüfus algoritmanın tekrarlanmasıyla azalır (çiftleşme sezonunun yararı olarak, başarılı eşleşmeler sayesinde bekar erkek ağaçkakan sayısı azalır). Bu süreç istismara yol açar.
7. İlk tekrarlarda (çiftleşme sezonunun başlarında), dişi ağaçkakanlar en uygun ve en yakın erkek ağaçkakandan etkilenir. Fakat son tekrarlarda sadece en iyi ağaçkakandan etkilenirler.
8. Basitleştirmek için, gpop davulunun yanı sıra, her bir dişi ağaçkakan zamanın belirli noktalarında sadece bir erkek ağaçkakanı yani dişi ağaçkakana en yakın erkek kuşu duyacak ve böylece davulun en yüksek ses yoğunluğuna sahip olduğunu farz edecek.
Üstte de değinildiği gibi, WMA algoritması ağaçkakanların çiftleşme davranışlarından ilham alan bir sürü zekası algoritmasıdır. Bilimsel açıdan WMA algoritması ile ateş böceği algoritması arasında bazı benzerlikler vardır. Fakat onların ikisi teknik ve işlem yönünden çok farklıdır. Ateş böceği algoritmasında ışık yoğunluğu kavramı iki ateşböceğinin etkilenme miktarı olarak tartışılır, aksine WMA algoritmasında ise ses yoğunluğu kavramı arama ajanlarının etkileme ölçümü olarak kullanılır. Bu iki kavram fizik kuralları ve formülleri bakımından oldukça farklıdır. FA algoritmasında nüfus üniseks olarak düşünülür ve her bir ateşböceği uydurma arama ajanları tarafından cezbedilebilir. Fakat WMA algoritmasındaki ağaçkakan nüfusu erkek ve dişi olarak düşünülür. Her bir dişi ağaçkakan en iyi ya da en yakındaki ağaçkakandan etkilenir. FA algoritmasının aksine WMA algoritması, algoritmanın performansı ve küresel ve yerel arama yetenekleri üzerinde önemli bir etkiye sahip istismar ve keşif aşamalarının verimli ve ardışık uygulanması için birkaç işlemi vardır.
2.3 Matematik Modeli ve Optimizasyon Algoritması
WMA algoritması dişi ve erkek ağaçkakan olarak iki faktörden meydan gelir. Erkek ve dişi ağaçkakanların her biri çözüm adayı olarak kabul edilir. WMA algoritmasında erkek ve dişi ağaçkakanlar cinsiyetlerine göre farklı değillerdir fakat amaç fonksiyonlarının değerlerine göre farklıdırlar. Ek olarak, erkek ve dişi ağaçkakanlar arsındaki fark problemler alanını keşfetme ve konumlarını güncelleme metotlarında bulunur. Dişi ağaçkakanlar problem alanına doğru hareket eden asıl arama ajanlarıdır ve erkek ağaçkakanlar onların uzağında en iyi konumdadır. Aslında, erkek ağaçkakanlar dişiler tarafından bulunan işaretler ve bayraklardır. Böylelikle, dişi ağaçkakanlar erkek kuşlar çevresinde ararlar ve onların lokasyonlarına göre konumlarını güncellerler. Eğer en iyi adayı bulurlarsa, erkek ağaçkakanın konumunu güncelleyecektir.

2.3.1 Başlangıç
WMA nüfusa dayalı bir algoritmadır. Her ağaçkakan çözüm adayı olarak düşünülür. Diğer meta-sezgisel algoritmalar gibi önerilen algoritma rastgele seçilen ağaçkakan grubunu kullanıma hazırlar. Aslında ağaçkakanlar arama alanına benzer şekilde dağıtılır. Her ağaçkakan problemin n-boyutlu çözüm vektörüdür. Algoritmanın maksimum iterasyon, nüfus büyüklüğü, RA olasılığı ve ses dalgalarının gücü gibi parametreler bu adımda ayarlanır. Fig. 1 önerilen WMA algoritmasının sözde kodunu gösterir.
2.3.2 Ağaçkakan Popülasyonunu Bölme ve Değerlendirme
Diğer kuşlar gibi ağaçkakanlar da en iyi eşi seçme eğilimindedir. Böylece en iyi genç ağaçkakan doğabilir. Bu adımda ağaçkakan popülasyonu onların zindelik değerlerini açıklayan amaç fonksiyonla değerlendirildi. Daha sonra ağaçkakan popülasyonu erkek ve dişi gruplara bölündü. Her bir iterasyonun başında ağaçkakan popülasyonu amaç fonksiyonlarına göre uydurma değerlerin oran esası ve erkek ağaçkakanların popülasyonunun orantısal büyüklüğü üzerinden sınıflandırılır, en nitelikli ağaçkakanların erkek kuşlar olduğu kabul edilir. Her bir iterasyon da erkek ağaçkakanlar amaç fonksiyonuna göre en yüksek zindelik derecesiyle arama ajanlarıdır. En yüksek zindelik derecesiyle erkek ağaçkakan en iyi gpop olarak seçilir. Bütün dişi ağaçkakanlar en iyi etkileyen ağaçkakan gpop’un mesafesine göre onun davul sesinin yüzdesini duyar ve ona doğru hareket eder.
2.3.3. Ağaçkakanların Hareketi
Bu adım da her ağaçkakan aşağıdaki eşitliğe göre konumlarını günceller (2.4).
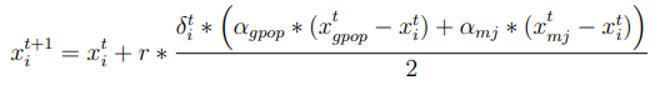
Buradaki xti ağaçkakanın önceki konumunu gösterir ve xtgpop en iyi üyenin konumunu gösterir. Dahası, xtmj erkek ağaçkakanın konumudur, r [0, 1] aralığından seçilen benzerlik dağılımının rastgele sayısıdır,
gti t iterasyonunda ağaçkakan için i-th katsayısını gösterir. Katsayıların değeri eşitliğe göre algoritmanın iterasyon döngüsü boyunca uyarlamalı olarak hesaplanır (2.5). a(agpop, amj) eşitlik boyunca kararlı olabilir (6). Aslında a bir dişi ağaçkakanın bir erkek ağaçkakandan alınan sesin yoğunluğuna göre ne kadar etkilendiğini gösterir.
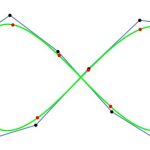
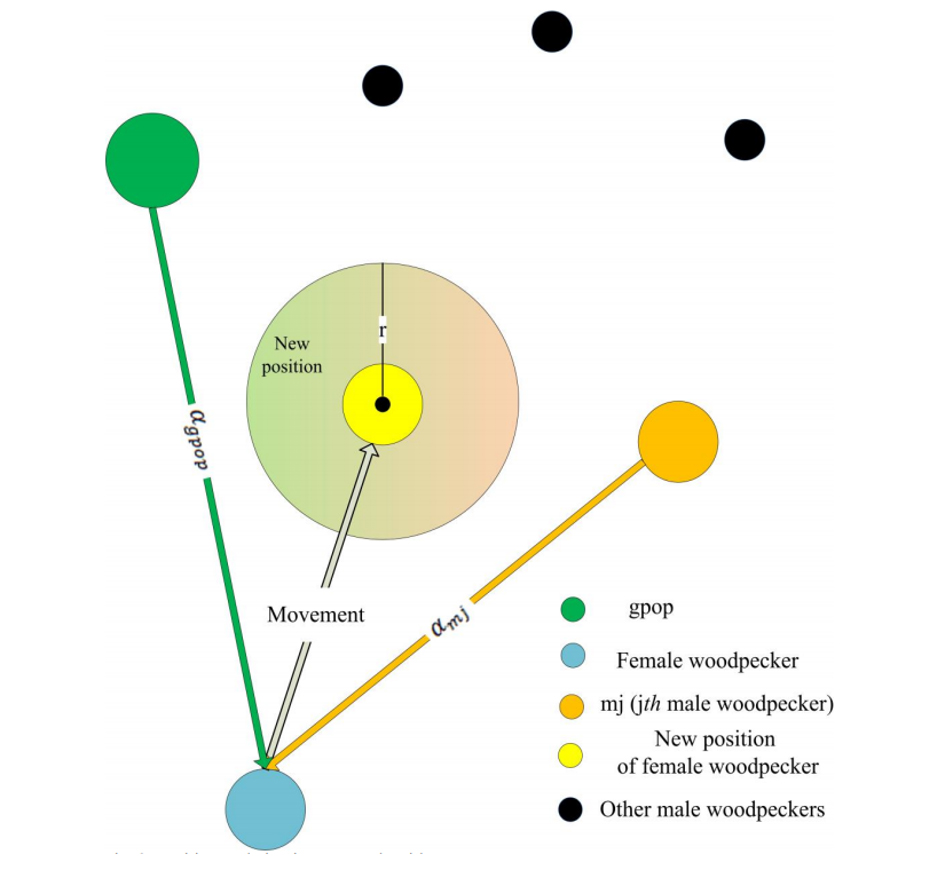
Önceki bölümün başında değinildiği gibi, dişi bir ağaçkakan eşleşme sezonunun her bir bölümünde sadece gpop olan ağaçkakandan değil aynı zamanda en yakın ağaçkakanın davul sesinden etkilenebilir. 2.4’teki eşitlikte verilen xmj erkek ağaçkakanın konumunun göstergesidir. Aslında her dişi ağaçkakan gpop ve mj olarak seçilen ağaçkakana göre konumunu günceller. Erkek kuştan mj değerinin seçilmesiyle ilgili, dişi ağaçkakanın her erkek kuştan Öklit mesafesi eşitlik boyunca her bir iterasyon için belirlenir (2.3). Sonra dişi kuştan en yakın uzaklıkta olan erkek kuş mj olarak seçilir. Aslında gpop popülasyondaki en iyi erkek kuşu gösterir. Sonuç olarak o dişi kuşu etkileyen davul sesini en yüksek kaliteyle oluşturur. Erkek kuş mj dişi kuşun yanındadır, böylece dişi kuşu etkilemek için ağacı oyar ve belirli arzularının geliştirmesini sağlar. Fig. 2 iki boyutlu arama uzayında mj ve gpop’a göre dişi ağaçkakanların konumlarını nasıl güncellediğini gösterir.
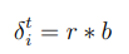
Bu eşitliğe göre r [0, 3] arasında rastgele dağılımdan rastgele bir sayıdır. b parametresinin değeri algoritmanın iterasyon döngüsü boyunca 0.77’den 0’a kadar düşer. Bu eksilmeyle keşif ve istismar aşamaları sırasıyla etkili bir şekilde uygulanır. Algoritmanın her bir iterasyonunda b’nin değeri 2.7’deki eşitlik kullanılarak hesaplanır.
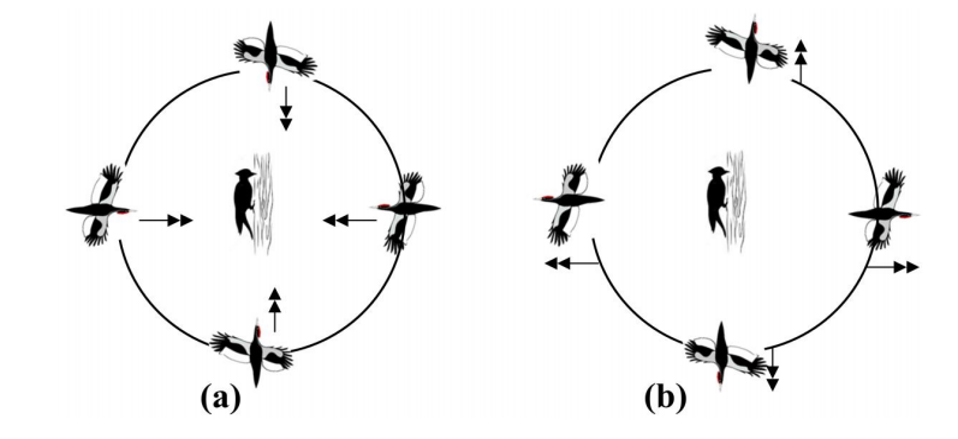
gti algoritmanın iterasyon döngüsü boyunca azalan b değerinin dalgalanma değerinin yanı sıra gti değeri [0, 3b] aralığında azalan rastgele bir değerdir. Eğer gti ‘nin değeri [0, 1] dağılımındaysa, dişi ağaçkakanın yeni konumu hedef ağaçkakanın konumu ile şimdiki konumu arasında herhangi bir rastgele noktaya yerleştirilmiştir. Diğer bir deyişle dişi ağaçkakanlar hedef ağaçkakana yaklaşır ve birleşir. Bu uygulama iterasyonun sonunda özellikle istismar aşamasını vurgular. Bu durumda, arama ajanları alınan çözümlerin kalitesini arttırmak amacıyla erkek ağaçkakanların çevresinde gelecek vaat eden alanları bölgesel aramak için talep edilir. Başka bir yönden, eğer gti >1 ise dişi ağaçkakan hedef ağaçkakandan uzaklaşması gerekir ve ondan uzaklaşır. Gelecek vaat eden alanların keşifleri için bu sonuçlar en iyi çözümlerdir. Bu durumda WMA algoritması küresel olarak araştırabilir. Kısacası, gti <1 ise dişi ağaçkakanlar hedef ağaçkakanla birleşirler (Fig. 3a), aksi takdir de ondan uzaklaşırlar (Fig. 3b).
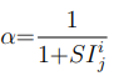
Bu eşitlikte a dişi ağaçkakanlara ulaşan i’yi ve hedef ağaçkakanın sesinin yoğunluğunu SIij’yi ağaçkakan için erkek ağaçkakanların etkileme olasılığını gösterir. Aslında a parametresi seçilen erkek ağaçkakanın cazibesine göre hızın miktarıdır. Hız sesin yoğunluğuyla ters orantılıdır. Başka bir deyişle ağaçkakanın varacağı yerin en yüksek ses yoğunluğu dişi ağaçkakan için en büyük payda olacaktır. Böylece hız azalacaktır. Hız [0, 1] aralığından seçilir. En yüksek değer ağaçkakanın menzili sıfıra yaklaştığında elde edilir. En düşük hız ağaçkakanın daha doğru bir şekilde menzile doğru hareket etmesidir. Bir ağaçkakan doğru tahmini çözümler içeren sonuçlar ve istismarın azaldığı merkezi hedef çevresinde hareket eder. Böylece a parametresi algoritmanın istismarı üzerinde bir etkiye sahiptir.
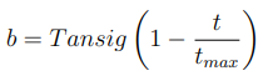
Burada Tansig teğet sigmoid fonksiyonudur, t şimdiki iterasyon sayısı ve tmax iterasyonun maksimum sayısıdır.
Erkek ağaçkakan nüfusu uyarlamalı olarak iterasyon döngüsü algoritması boyunca azalır. Son iterasyonda sadece bir erkek ağaçkakan kalır. Erkek ağaçkakanların sayısının çokluğu ilk iterasyonda keşfi arttırabilir. Dahası, algoritma en uygun yerel bölgeye sıkışıp kalmaktan korunur. Son iterasyonda azalan erkek kuşların sayısı istismarı ve çözümün doğruluğunu arttırır. Eşitlik 2.8 her bir ağaçkakanın sayısını açıklamak için kullanılabilir.
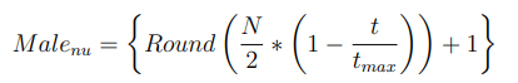
Bu eşitlikte Malenu her bir iterasyondaki erkek ağaçkakan sayısıdır ve t şimdiki iterasyon sayısıdır. Dahası, ağaçkakan nüfusunun maksimum miktarını N gösterdiğinde tmax iterasyonun maksimum sayısını gösterir. Erkek ağaçkakanlar için en az nüfus bir ağaçkakandır ve O’da gpoptur. Bu durumda 2.4’teki eşitlik 2.9’daki eşitliği basitleştirir (2.9).

2.3.4 Kaçma İşlevi
Bir dişi ağaçkakan başka bir erkek ağaçkakanın sesinden etkilendiğinde ve ona doğru hareket ettiğinde sesler doğada benzeşebilir. Böylece erkek ağaçkakanlar bilinçsizce yolları değiştirebilir ve sapabilirler. Diğer yandan bir ağaçkakan diğer ağaçkakanlardan ve yol üstündeki avcı kuşlardan etkilenebilir. Ayrıca yolda tehlikeli hissetmesinden dolayı rastgele değişiklikler olabilir. Rastgele değişiklikler kaçma işlevi olarak simüle edilir. Diğer yandan yol değişiklikleri çözümüm rastgele değişikliği gibi değerlendirilir. Ağaçkakanların nasıl çıktıkları popülasyonun en iyi üyesinden alınan sesin yoğunluğuna göre farklı olabilir. Bu bölümde hareketin iki türü ağaçkakanların kaçışı olarak düşünülür. Seçilen hareket türünün değer ölçütü gpop’tan alınan ses yoğunluğunun eşiğine göredir (THa). Ha’nın değeri 2.11’deki eşitliğe göre hesaplanır. Önceki bölümde neyle göre olduğu belirtilen Ha’nın değeri sesin yoğunluğuyla ters orantılıdır. aigpop en büyük değeri davul sesinin kalitesinin düşüklüğü ve ağaçkakan ile gpop arasındaki mesafenin büyüklüğüdür. Eğer aigpop >Ha ise ağaçkakanın gpop’tan uzakta olduğu varsayılır ve davul sesi çok düşük ses yoğunluğuyla alınacaktır. Bu durumda dişi ağaçkakanlar gpop’a göre uygunsuz bir noktadadır, bu yüzden arama uzayının başka bir noktasına 2.10’daki eşitliğe göre oldukça rastgele uçarlar. Bu hareket rastgele kaçış (RRA) olarak adlandırılır.
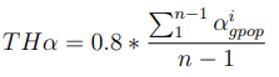
Ha ilk iterasyonda hesaplanan gpop ses yoğunluğunun eşiğidir, n ağaçkakanların boyutudur ve aigpop 2.6’daki eşitlik kullanılarak hesaplanan değer i ağaçkakanların ses yoğunluğunun orantılı hesaplanmasıdır.
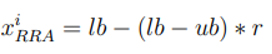
Bu eşitliğe göre xiRPA ağaçkakan üzerinden RRA ile elde edilen yeni elementin konumudur, [0, 1] aralığından seçilen tekdüze sürekli dağıtımın rastgele sayısıdır. lb ve ub sırasıyla sınır değerlerinin en düşük ve en yüksek değerleridir. Eğer aigpop < Ha ise ağaçkakan uygun ses yoğunluğuyla gpop’ın davulunun sesini duymuştur. Böylece o uygun konumdadır. Bu durumda ağaçkakan gpop’a kaçar. Bu kaçış gpop’a kaçış (Gpop Running Away) olarak adlandırılır. GRA oranı RA olasılığı ile kontrol edilir (PGRA). PGRA ‘nın değeri eşitlik 2.12’deki formülle algoritmanın iterasyon döngüsünde y’dan 0’a uygun bir şekilde azalır (2.12).
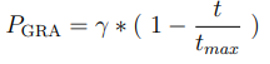
t şimdiki iterasyon sayısıdır. tmax iterasyonun maksimum sayısını gösterir, y ise RA katsayısıdır. Önerilen algoritma GRA iki ebeveyn ile gerçekleştirilir. GRAbit 2.13’ deki eşitlikle elde edilen elementlerden oluşan problem boyutu olduğu sürece bir vektördür.
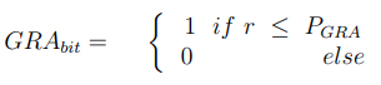
Bu eşitlikte, r vektör elementidir. Her element [0, 1] aralığından seçilen tekdüze dağılımın rastgele bir sayısıdır. WMA algoritması 2.14’ teki eşitliğe göre bitirilir.
GRA işlemcisi dişi ağaçkakan gpop’a kaçar. Diğer etkileyen faktör ise rastgele seçilen ağaçkakanın konumudur (xr). Bu ağaçkakan popülasyonundan rastgele seçilir amaç dişi ağaçkakanların kaçışını rastgele dağıtmaktır. Aslında dişi ağaçkakan gpop’a ve ağaçkakanın rastgele konumuna kaçar. Dişi ağaçkakanın yeni konumu gpop’un konumu ve rastgele ağaçkakanın konumu arasında herhangi bir noktada konumlanır.
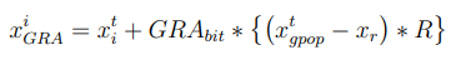
Bu eşitlikte xiGRA ağaçkakan üzerinde RA’den elde edilen yeni elementin konumudur, xr ağaçkakanın rastgele konumudur. xtgpop t’ inci iterasyonda en iyi üyenin konumunu gösterir. xit iterasyonda ilk adımda taşınan arama uzayıyla elde edilen ağaçkakanın yeni konumudur. R [-1, 1] aralığından seçilen tek düze dağılımın rastgele sayısıdır. GRAbit vektörünün her bir elementi 2.14’ teki eşitliğin ikinci ifadenin bir değeridir. Bu işlemin sonunda xiGRA ya da xiRRA zindeliği hedef işlem kullanılarak hesaplanır. Eğer zindelik değeri xit’ den daha iyiyse yerini değiştirir. Aksi takdirde element RA işlemi tarafından görmezden gelinerek oluşturulur. Verilen Ha değeri ve WMA algoritmasının yaşam döngüsü içinde ilk iterasyonlarında a’dan daha geniş değerlerin RRA oluşum oranı bu iterasyonda en yüksektir. RRA’ den beri dişi ağaçkakanların arama uzayı çevresinde rastgele uçmaları keşfin sonucudur. Algoritma döngüsü daha fazla tekrar ettikçe dişi ağaçkakanların gpop’a yaklaşımından dolayı a’nın oranının azalmasının yanı sıra RRA oranı azalır ve GRA oranı artar. GRA işlemcisi dişi ağaçkakanların gpop çevresindeki rastgele hareketi ve aynı zamanda başka rastgele ağaçkakanın keşfinin artmasıdır. Algoritmanın iterasyon döngüsü boyunca azalan PGRA ile rastgele hareketin azalmasına rağmen, iterasyonun sonunda yerel en uygunluktan hala kaçınabilir. Azalan PGRA ile iterasyonun sonunda istismar gerektiğinden dişi ağaçkakanlar istismara yol açarak daha fazla konumlarına konsantre olurlar. Özet olarak, RA fonksiyonu ilk iterasyonda keşfin uygulanması üzerinde ve bölgesel uygunlukla durgunluğu önlemek için büyük bir etkiye sahiptir.

2.3.5 Evrimsel Yeni Konum ve Bitirme Şartlarının Kontrolü
Bu adımda ağaçkakanın yeni konumu önceki konumu ve en iyi ağaçkakanın konumu ile kıyaslanır. Eğer konum birinden daha iyiyse konum değişecektir. Eğer algoritmanın bitirme şartları karşılandıysa en iyi çözüm problemin en uygun çözümü olarak seçilecektir. Aksi takdirde adımlar 3-5 kez tekrar edecektir.
3. Kıyaslama Fonksiyonlarıyla Evrimsel WMA Algoritması
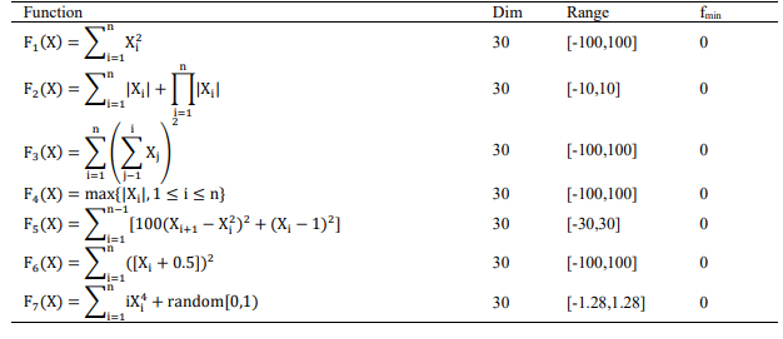
Bu bölümde önerilen algoritmanın verimliliği 19 matematiksel kıyaslama fonksiyonu üzerinden değerlendirildi ve üç gruba ayrılmıştır: tek modlu (Tablo 1), çok modlu (Tablo 2), bileşik fonksiyon (Tablo 3). Tek modlu fonksiyon sadece bir tane en uygun değere sahip. Algoritmanın yakınsaması ve istismarın değerlendirilmesi için uygun fonksiyondur. Fakat çok modlu fonksiyon birden fazla optimuma sahiptir. Tek modlu fonksiyondan daha fazla zorludur. Optimumların biri küreseldir ve onların sonuncusu bölgesel optimumdur. Her algoritma küresel optimumu belirlemek ve yaklaşmak için bütün bölgesel optimumlardan kaçınmalıdır. Böylece, çok modlu fonksiyon testi bölgesel optimumdan kaçınma ve keşfin içinde algoritmanın performansını değerlendirmek için kullanılabilir. Kıyaslama fonksiyonlarının sınıfı bileşik fonksiyonları içerir. Aslında bu fonksiyonlar çok modlu ve tek modlu fonksiyonların birleştirilmiş, kaydırılmış, onaylanmış ve ön yargılı versiyonudur. Bu fonksiyonlarda arama uzayı çok karışıktır çünkü birçok bölgesel optimumu vardır ve arama uzayının farklı alanları farklı formlar içindedir. Böyle bir fonksiyonda, bir optimizasyon algoritması istismar ve keşif arasındaki yeterli dengeyi kurabilir ve küresel optimuma doğru hareket edebilir. Böylece bu fonksiyonların asıl görevi keşfi ve istismarı eşzamanlı olarak değerlendirmektir [4,46]. Önerilen algoritma Genetik Algoritma (GA), Parçacık Sürüsü Optimizasyonu (PSO), Ateşböceği Algoritması (FA) [8], Saten Çardak Optimizer (SBO) [30], Yapay Arı Kolonisi (ABC) [47], Wolf Optimizer (GWO) [5], Çoklu- İşaret Optimizer (MVO) [3] ve Yarasa Algoritma (BA) [43] gibi çok iyi bilinen yeni grup meta-sezgisel algoritmalarla karşılaştırıldı.
Testlerin hepsi MATLAP 2017a’ da çalıştırıldı. Her kıyaslama fonksiyonu optimizasyon algoritmalarıyla 30 kez çalıştırıldı. 30 uygulamanın en iyi sonucu standart sapma (Std) ve ortalamalar (Ave) karşılaştırılarak hesaplandı. Sonra Wilcoxon işaretli sıralama testleri WMA ve diğer algortimalar arasındaki önemli farkları analiz etmek için kullanıldı. Çıktı p-değeri istatiğidir.
Bu çalışmada, önem seviyesi 0.05 olarak kullanılmıştır. Böylece eğer iki algoritmanın sonuçları 0.05’ten düşükse onlar istatiksel olarak farklıdır. Bütün algoritmalarda ilk popülasyonun büyüklüğü 50’dir ve maksimum iterasyon 500’dür. Problemin boyutu 30’dur. Tablo 4’te her bir algoritma için diğer parametre düzenlemeleri gösterilmektedir.

3.1 İstismar Kapasitesinin Evrimi
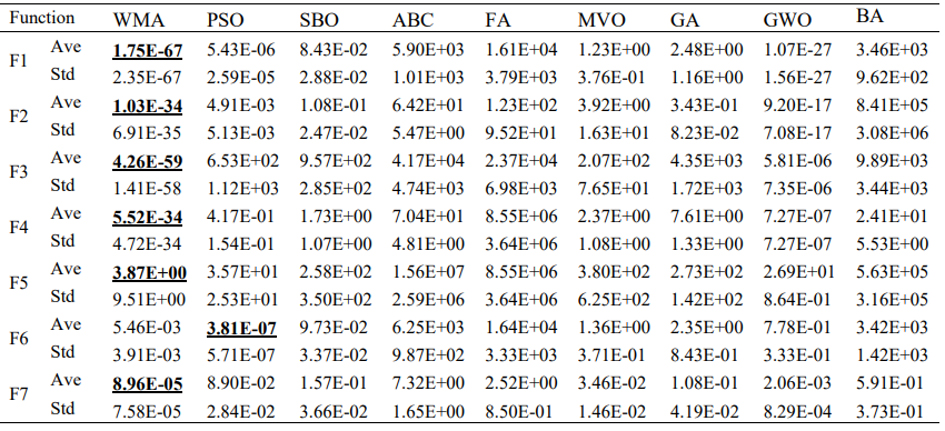
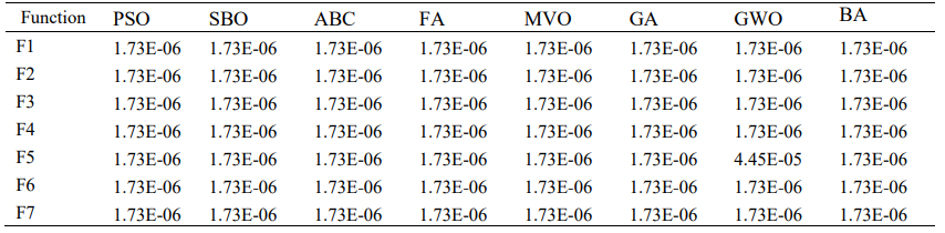
Tablo 5 optimizasyon algoritmasının tek modlu kıyaslama fonksiyonunun derleme sonucunu gösterir. Buna göre, WMA algoritması 7 tek modlu fonksiyon üzerinden 6’sında diğer algoritmalardan daha iyi sonuçlar göstermiştir. Bu fonksiyonun verilen özellikleriyle, sonuçlar önerilen algoritmanın fazlasıyla istismar etme kabiliyetini gösterir. Figür 4’te göre WMA algoritması fazlasıyla sömürebilirliğine ek olarak diğer algoritmalardan daha hızlı yakınlaşma performansı gösterdi. Tablo 6’da Wilcoxon işaretli sıralama testleri görülebilir. Ek olarak bütün p-değerleri 0.05’ten küçüktür. Böylece WMA ve diğer algoritmalar arasında önemli bir fark vardır.
3.2 Keşif Kapasitesinin Evrimi (Fonksiyon F8-F13)
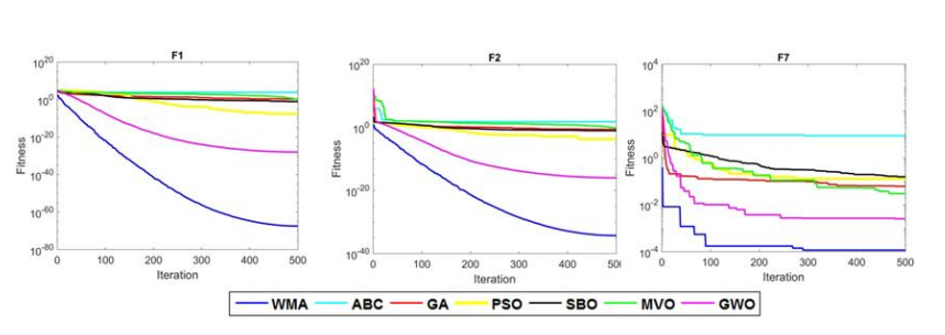
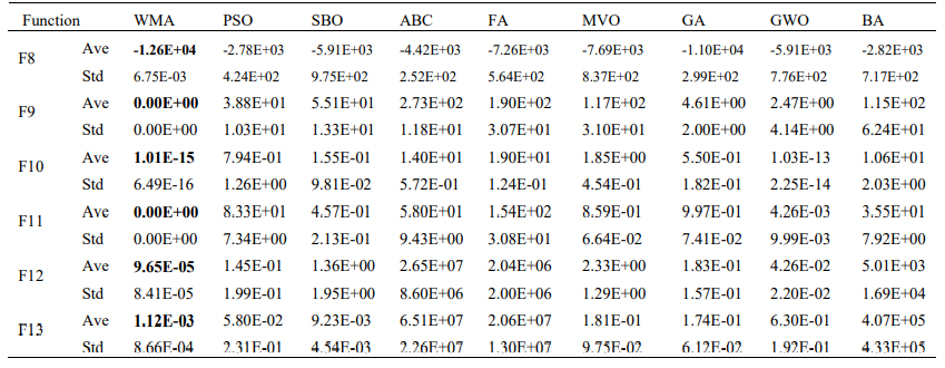
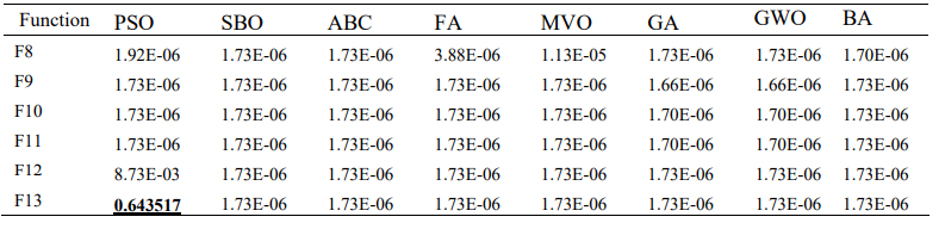
Tablo 7 optimizasyon algoritmalarında 6 çok modlu fonksiyonların derlemenin sonuçlarını gösterir. Buna göre WMA algoritmasında çok modlu fonksiyonlar bütün test durumlarında en iyi performansı gösterdi. Ayrıca Tablo 8 Wilcoxon işaretli sıralama testleri içinde optimizasyon algoritmalarının karşılaştırılmasını gösterir. Bir fonksiyon dışında bütün durumlar için p-değeri 0.05 değerinin altındadır. Böylece WMA ve diğer algoritmalar arasında önemli bir fark vardır. Figür 5’te çok modlu fonksiyonlar içinde optimizasyon algoritmalarının sırasıyla yakınlaşma diyagramını gösterir. WMA algoritması yüksek keşif kabiliyeti ve küresel optimuma doğru hareketi sonucuyla bölgesel optimumdan kaçınmasından dolayı diğer metotlardan daha çok yakınlaştı.
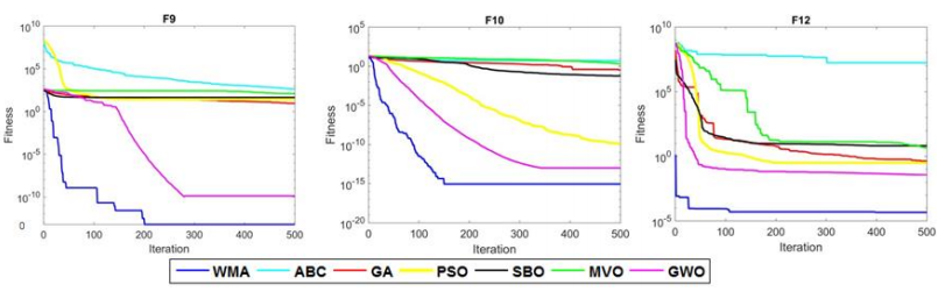
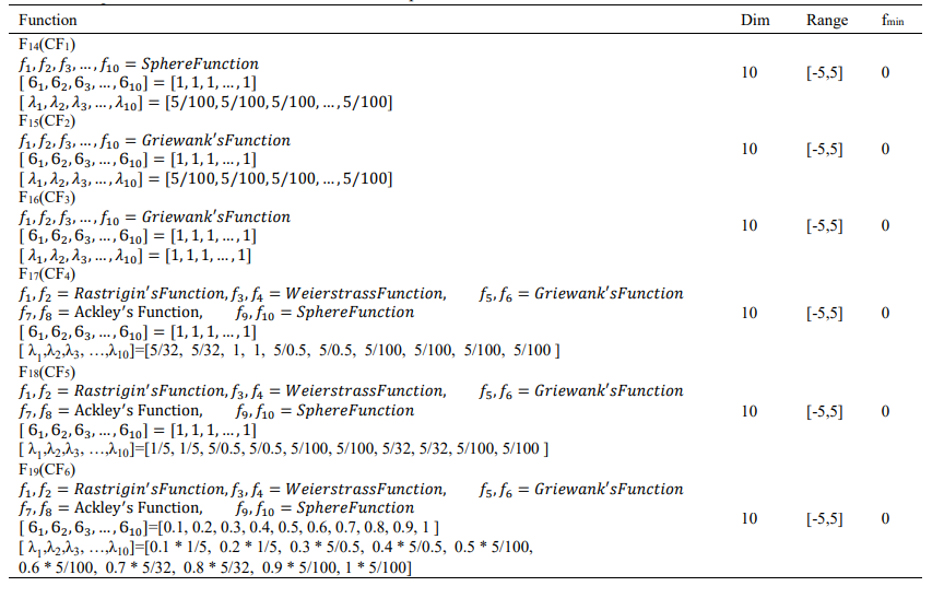
3.3 Bölgesel Minimumdan Kaçış Yeteneği (Fonksiyon F14-F19)
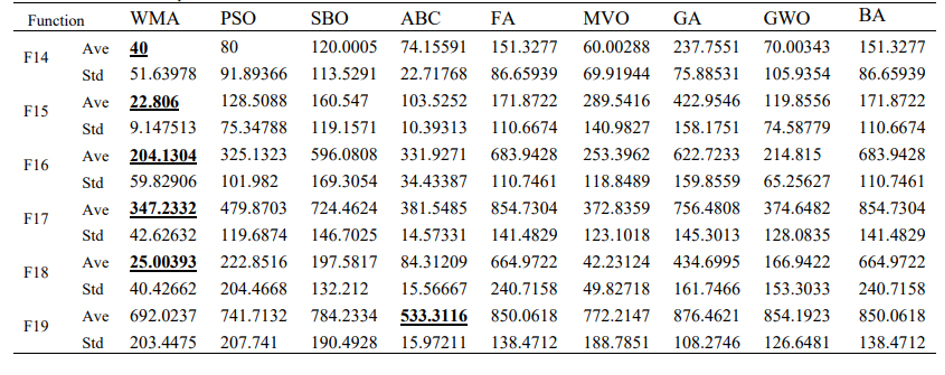
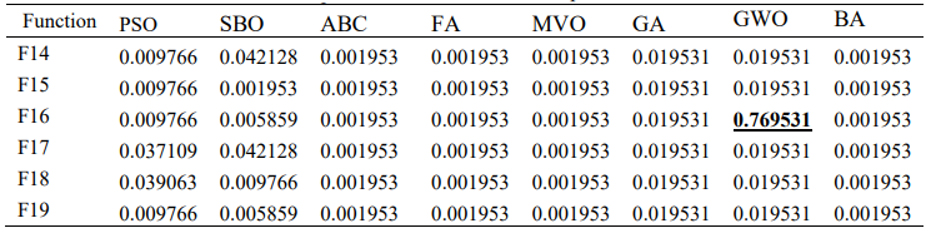
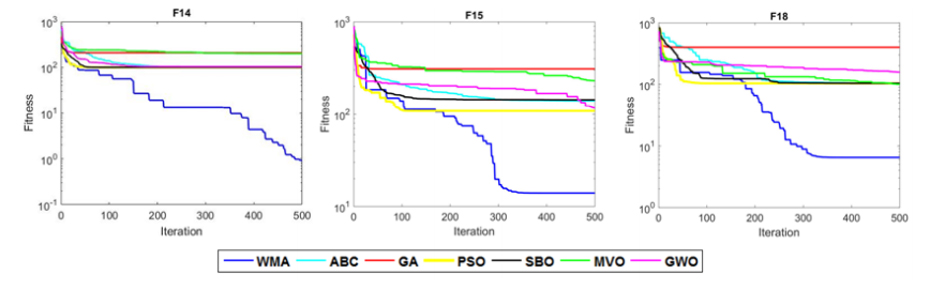
Bileşik fonksiyonlar da bir optimizasyon algoritması keşif ve bölgesel optimumdan kaçınmaya izin veren sömürü arasında etkili bir denge kurar. Tablo 9 optimizasyon algoritmasında derlenen 6 bileşik fonksiyonun sonuçlarını gösterir. Buna göre fonksiyonlar WMA algoritmasında test durumlarının çoğunluğu üzerinden en iyi performansı gösterir. Ayrıca tablo 10 Wilcoxon işaretli sıralama testleri içinde optimizasyon algoritmalarının karşılaştırmasını gösterir. p-değeri F16’nın dışındaki çoğu durumda 0.05’ten daha küçüktür. WMA ve diğer algoritmalar arasında önemli bir fark vardır. Sonuçlardaki büyük farklılık değerlendirilen bileşik fonksiyonda arama uzayının fazla karışık olmasından dolayıdır. Figür 6 optimizasyon algoritmalarının kesişim diyagramıdır. WMA algoritması önceden tartışılmış olarak diğer algoritmalarla birleştirildi, keşif ve istismar aşamaları bileşim fonksiyonu içinde kombine edildi. Figür 6 ve tablo 9’un sonuçlarına göre önerilen algoritma böylesine karışık arama uzayının çeşitli farklılıklarını ele alan iki aşama arasında etkili bir denge kurdu.
3.4 WMA Kullanarak Large-Scale Problemlerinin Optimizasyonu
WMA algoritmasının yeteneklerini ve uygulanan algoritmanın önemini göstermek için yüksek boyutlu, gerçek dünya problemleri, tek modlu ve çok modlu kıyaslama fonksiyonlarının (F1…F13) 1000 boyutlu versiyonları kullanıldı. Bu testte popülasyonun büyüklüğü ve iterasyon sayısı sırasıyla 30 ve 500 olarak kabul edildi. İstatiksel sonuçlar 30 bağımsız çalışanın ortalamışıdır. Tablo 11’de bu problem testinin detayları rapor edilmiştir. Tek modlu ve çok modlu yüksek boyutlar için önerilen algoritmanın sonuçları tablo 11’ de sunulmuştur. Görüldüğü gibi sonuçlar, problem çeşitlerinin sayısı arttırıldığında bahsedilen yüksek boyutlar içinde fazlasıyla etkili ve gelecek vaat ediyor. 1000 boyutlu arama uzayının sonucu tablo 11’ de verildi. Görüldüğü gibi WMA algoritması tüm F11 ve F13 fonksiyonları için en iyi sonuçları sunan algoritmalardan daha iyi performans gösterir. Önerilen algoritmanın 30 ve 1000 boyut içinde F9 ve F11 fonksiyonları için küresel optimum da elde edildiği belirtilmelidir.
4. Sonuç
Bu çalışmada WMA olarak adlandırılan yeni bir meta-sezgisel algoritması çiftleşme sürecinde ağaçkakanların davranış zekasından esinlenir. WMA algoritmasında alınan davul sesi yoğunluğu başka bir yöne hareket etmek için cezbedici olarak adlandırılır. Ses yoğunluğu ses dalgaları fiziğinin kavramlarından esinlenir. Önerilen algoritma arama uzayını keşfetmek ve kullanmak için birçok işlemciyle donatılmıştır. WMA algoritmasında popülasyon erkek ve dişi ağaçkakan olarak bölünmüştür. Dişi ağaçkakanlar konumlarını en yakın ve en iyi erkek kuşa göre güncellerler. İlk iterasyonda metot keşfi ve çeşitliliği arttırır. Son iterasyonda erkek ağaçkakanların sayısındaki uyarlanabilir azalma sonuç olarak ortaya çıkan çözümlerin çevresinde istismar azalır. Aynı zamanda iterasyon döngüsünde algoritma boyunca uyarlamalı olarak adımların büyüklüklerinin azalması keşfi ve istismarı ayrıca iki aşama arasındaki transferi dorudan etkileyecek.
Önerilen algoritmanın verimliliği 19 matematiksel kıyaslama fonksiyonu kullanılarak değerlendirildi (7 tek modlu, 6 çok modlu, 6 bileşik). WMA algoritması yeni ve çok iyi bilinen meta-sezgisel algoritma grubuyla karşılaştırıldı. Önerilen algoritmayla 17 kıyaslama fonksiyonunda en iyi sonuçlar elde edildi. Algoritma konveks olmayan, ayrılmayan ve ölçeklenebilir fonksiyonlar içinde önemli sonuçlar üretti. Ek olarak karşılaştırma diyagramları yüksek kıyaslama hızını gösterdi. Simülasyon sonuçları algoritmanın arama uzayını keşfetmek ve kullanmak için yüksek yeteneklerini gösterdi. Ayrıca algoritma hızlı bir şekilde kıyaslama sağlayabilir. Gelecek çalışmalara öneri olarak WMA gerçek dünya problemlerini çözmek için farklı mühendislik alanlarında kullanılabilir. Aynı zamanda WMA algoritmasının performansını geliştirmek için diğer algoritmalarla birleştirilebilir.